رج هانوی , معمایی است که از سه میله و N دیسک با اندازه های متفاوت . فرض شود که اگر دیسکی روی یک میله باشد , فقط دیسکی که قطر آن کوچکتر است می تواند بالای آن قرار گیرد مسئله چنین است که هر بار فقط یک دیسک انتقال یابد .
را حل : این مسئله با استفاده از یک الگوریتم باز گشتی حل می شود .
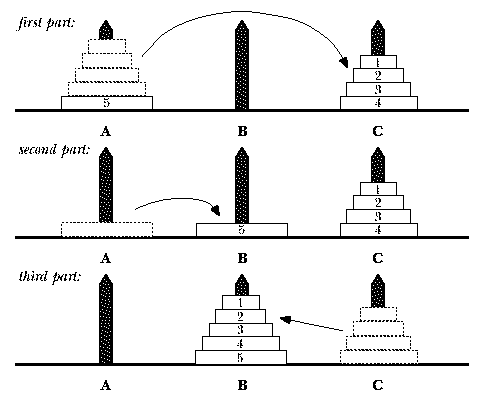
-اگر فقط یک دیسک باشد آنگاه آن را به میله مورد نظر انتقال می دهیم .
-اگر n > 1 باشد ; برای این کار n-1 دیسک بالای میله 1 را به میله 2 انتقال می دهیم . حالا دیسک پایینی میله 1 را ثابت باقی می ماند . حال دیسک باقیمانده در در میله 1 را به میله 3 منتقل میکنیم . سرانجام بار دیگر بصورت بازگشتی الگوریتم را فرا خانده تا n - 1 دیسک میله دو را به 3 منتقل کند .

اکنون موفق شدیم n دیسک را از میله 1 به 3 منقل کنیم .این مسئله در درسهایی مانند ساختمان گسسته و ساختمان داده مورد بحث وبررسی قرار می گیرد .

کد php الگوریتم:




[IMG]http://www.cs.berkeley.edu/%7Ebh/v1ch8/hanoi4.gif[/IMG]/*Algorithmic solution is as follows

1) if TopN==1, move the single disc from A to C and stop.2) Move the top n-1 discs from A to B, using C as Inter.3) Move the remaining disc from A to C.4) Move the n-1 discs from B to C, using A as destination(dest).
*/
#include 
#include void  tower(int,char,char,char); /*prototype*/int main()
{int ndisk;clrscr();printf("\n Enter number of disks <<<::: ");scanf("%d",&ndisk);tower(ndisk,'A','B','C'); /*Calling Function*/getch();
return 0;

} /* End of program */

/********************************************/

// src = Source | aux = Auxiliry | dest = Destinationvoid tower(int topN, char src,char aux,char  dest)
{
if(topN == 1)
{printf("\n Disk 1 from %c to %c ",src,dest);
}
else
{tower(topN-1,src,dest,aux); //src to auxprintf("\n Disk %d from %c to %c ",topN,src,dest);tower(topN-1,aux,src,dest); //aux to dest}
}